해석학 공부하기

새벽에 이야기했던대로 새로운 프로젝트는 오늘부터 시작하게 된다. 첫 번째 단계는 해석학의 내용을 완벽하게 이해하는 것이므로, 오늘부터 바로 공부에 착수할 것이다.

진행 방식

우선 책에 나오는 모든 정의 (Definition), 정리 (Theorem), 따름 정리 (Corollary), 비고 (Remark) 등의 내용을 모두 정리할 것이며, 정리나 따름 정리 등은 직접 증명하는 것도 시도해볼 것이다.

이 과정에서 종이에 많은 수식들을 적게 될 것이고, 풀이과정 등이 담기게 될 것이다. 글에 마지막에 이 종이들을 스캔하여 만든 PDF를 넣어둘 것이다. 또한 각 내용들에 대하여 내가 이해한대로 나름대로 설명을 제공할 것이며, 최대한 흥미롭게 전달하고자 노력을 하겠다.

1단원 공부 시작

오늘부터 다룰 내용은 1단원의 내용으로, 단원의 이름은 The Real and Complex Number Systems 이다. 이 단원은 총 9개의 소단원으로 구성되어 있다.

1. Introduction: 유리수 만으로는 현실의 여러 수들을 나타내기에 충분하지 않음을 보이며 실수체계가 필요한 이유를 제시한다.

2. Ordered Sets: order가 무엇인지 정의하며 이런 관계를 가지는 집합인 Ordered Set에 대하여 정의한다.

3. Fields: Field가 무엇인지 정의한다.

4. The Real Field: 앞에서 정의한 Ordered Set과 Field의 정의를 활용하여 실수체를 정의한다.

5. The Extended Real Number System: 확장된 실수체를 정의한다. 여기서 무한대라는 것이 무엇인지 정의한다.

6. The Complex Field: 복소수체를 정의한다.

7. Euclidean Spaces: ‘유클리드 공간’이 무엇인지 정의한다. 이름은 어려워 보이는데 내용은 익숙할 것이다.

8. Appendix: 부록이다. 이 부록에서는 ‘cut’이라는 개념을 이용하여 실수체를 구성해볼 것이다.

9. Exercises: 배운 개념을 활용하여 풀어볼 연습문제들이다.

오늘은 이 9개의 소단원을 모두 다루어볼 것이다. 첫날이라 쉬운게 걸린만큼, 이정도는 다 해낼 수 있어야 해석학 게임 프로젝트를 진행하는데 차질이 없을 것이다.

(수정: 2023-12-30) 역시 택도 없는 소리였다. 해석학 내용은 워낙 방대하고 어려운 만큼 페이스를 좀 더 길게 잡아야 했다. 해석학 게임 프로젝트는 초장기 프로젝트라고 보는 것이 좋겠다.

Introduction

앞서 이야기한 것처럼, 현실의 여러 가지 수를 나타내는데에 유리수 만으로는 충분하지 않다. 가장 대표적인 사례가 길이가 1인 직사각형의 대각선의 길이가 $\sqrt{2}$인 경우일 것이다.

나무위키에 따르면 유리수만을 수로 생각한 피타고라스는 이러한 무리수 길이를 수로 인정하지 않고 비밀로 부쳤으나 히파소스가 그 비밀을 대중 앞에서 폭로하자 그를 암살했다는 일화가 있다. 요즘은 무리수가 널리 인정되는 시대인 만큼 이런 글을 쓴다고 해서 암살 당할 걱정은 없으니 천만다행이다.

어쨌든 원래 이야기로 돌아와서 아래의 내용을 살펴보자.

1.1 Example

다음과 같은 방정식 \[p^2=2\]를 만족시키는 유리수 p는 존재하지 않는다.

해설

증명은 간단하면서도 잘 알려져 있다. 증명은 다음과 같다.

증명

우리는 귀류법을 이용하여 이 명제를 증명할 것이다. 귀류법이 무엇인지 간단하게 설명하면, 결론을 부정하였을 때 기존의 가정과 모순이 생김을 보임으로써 원래의 결론이 타당함을 보이는 증명 방법이다.

먼저 $p^2=2$를 만족시키는 유리수 $p$가 존재한다고 가정하자. 이 $p$는 유리수 이므로, 어떤 서로소인 두 수 정수 $m$과 $n$에 대하여 $p=m/n$의 형태로 나타낼 수 있다.

$p^2=m^2/n^2=2$ 이므로, $m^2=2n^2$이다. 여기서 알 수 있는 것은 $m$은 2를 약수로 가진다는 사실이다. 왜 그러한지는 조금만 생각해보면 알 수 있다. 쉽게 말하자면, 어떤 수를 두 번 곱했을 때, 그 수가 짝수이려면 짝수를 두 번 곱해야만 한다. 홀수를 두 번 곱해서는 짝수를 얻어낼 수 없는 것이다.

방금 $m$이 2를 약수로 가진다는 사실을 알아냈고, 이를 이용해서 어떤 정수 $k$에 대하여 $m=2k$로 나타낼 수 있다. $m^2=(2k)^2=4k^2=2n^2$ 이므로, $2k^2=n^2$이다. 앞에서와 같은 이유로, $n$ 또한 2를 약수로 가진다는 사실을 알 수 있다.

여기서 문제점이 생긴다. 처음에 우리는 $p$가 유리수라는 가정에 의해서 '서로소인' $m$과 $n$을 이용해 $p=m/n$과 같이 나타내었던 것인데, 이제와서는 $m$과 $n$이 모두 2를 약수로 가진다고 한다. 그렇다면 서로소가 아니게 된다. $p^2=2$를 만족하는 유리수 $p$는 없다는 '결론'을 부정한 탓에, 이러한 '모순'이 발생하는 것이다.

따라서, $p^2=2$를 만족시키는 유리수 $p$는 존재하지 않는다. $\blacksquare$

수학에 관심이 있는 사람이라면, 이 증명을 본적이 있을 것이다. 나도 고등학교 때 본 적이 있는 증명이다. 이 책에서는 한 가지 증명을 더 소개하는데, 이 글에서는 생략하도록 하겠다.

1.2 Remark

위와 같은 예시를 보인 것은 유리수로는 제대로 표현하지 못하는 ‘빈 공간’들이 존재함을 보임으로써 이러한 문제를 해결할 수 있는 실수 체계가 필요한 당위성을 제공하기 위함이다. 이러한 ‘빈 공간’없이 현실 세계의 수를 나타낼 수 있는 실수의 특성은 해석학에서 중요한 역할을 수행한다. 실수의 구조를 확립하기 위해서 아래에서는 표준적인 집합론에서 사용되는 용어들을 정의한다.

해설

…라고 책에 쓰여있었다. 원문의 의미를 모두 담아낸 것은 아니지만, 큰 흐름을 설명하는 데는 이정도로 번역하면 충분하다고 생각했다. 만약에 원문이 궁금하다면 어둠의 경로를 이용하거나 책을 직접 사서 읽으면 된다. 참고로 이 블로그에서는 libgen, z-library 등의 사이트를 이용하여 이 책의 PDF 파일을 구하는 등의 불법적인 활동을 권장하지 않는다. 실제로 필자는 이 책을 사서 가지고 있다!

1.3 Definitions

1. $A$가 숫자나 그 이외의 것들로 구성된 집합이라고 할 때, $x$가 $A$의 어떤 구성원 (혹은 요소)임을 나타내기 위해서 $x\in A$와 같이 나타낸다.

2. 만약 $x$가 $A$의 구성원이 아니라면, $x\notin A$와 같이 나타낸다.

3. 어떤 집합에 요소가 하나도 없다면 empty set (공집합) 이라고 부르며, 하나라도 있다면 nonempty 하다고 말한다.

4. 집합 $A$와 $B$가 있을 때, $A$의 모든 원소가 $B$의 원소일 경우, $A$는 $B$의 subset (부분집합) 이라고 부르며, $A\subset B$ 또는 $B\supset A$로 표현한다. 이 때, $B$의 원소 중에 $A$에는 포함되지 않는 것이 있을 경우, $A$는 $B$의 proper subset (진부분집합) 이라고 부른다. 참고로, 모든 집합은 자기자신의 subset이다.

5. 만약 $A\subset B$이고 $B\subset A$라면, $A=B$로 나타낸다. 그렇지 않으면, $A\neq B$로 나타낸다.

해설

이 위에 있는 내용들이 너무나도 당연한 이야기처럼 보일 수 있다. 왜냐하면 저런 식의 기호를 이미 고등학교 때부터 써왔기 떄문이다. 그렇다고 해석학의 모든 내용을 정리하는데 안 쓰기도 좀 그래서 넣어두었다. 만약 저런 기호들이 익숙하지 않다면, 앞으로 맨날 쓸 기호니까 질 익혀두길 바란다.

1.4 Definition

모든 유리수들의 집합을 $\mathbb{Q}$라고 표현한다.

해설

책에는 그냥 $Q$로 적혀있기는 했는데, 다들 칠판체로 표현하길래 나도 그냥 칠판체로 적어두었다. 참고로 저걸 Q라고 적는 이유는 영어단어 Quotient의 앞글자를 따서 그렇게 적는 것으로 알고있다. 여담으로, Quotient의 발음은 [큐오티언트], [쿼티언트] 같은 것이 아니라, [쿼션트] 라고 한다. 이 글을 읽는 독자들은 필자와 같은 어이없는 실수를 하지 않기 바란다.

여기까지가 Introduction 부분이었다. 이 소단원에서는 유리수에 ‘빈 공간’이 있다는 것을 보이면서 왜 실수가 필요한지 당위성을 제공하였다. 또한, 앞으로 자주 쓰게 될 집합론 관련 기호들을 정의해두었다. 9개의 단원을 다루어야 하고, 그 중에서도 제일 간단한 Introduction만 다루었는데도 벌써 지치는 것 같다. 또 당연한 소리만 계속 반복하는 것 같아 읽기 귀찮고 지루할 수 있다. 하지만 갈길이 머니 독자 여러분도 힘을 내주길 바란다. 아직 진짜 재밌는건 시작도 안했기 때문이다.

Ordered Sets

이 소단원에서는 Ordered Set이 무엇인지 정의할 것이다. 이 ordered라는 개념은 실수를 구성하는 큰 부품중 하나이다. 이번에도 당연한 소리만 하는거 아니냐고 생각할 수 있지만, 지금부터는 해석학이나 심화된 미분적분학을 공부하지 않은 사람이라면 처음 볼법한 용어들이 나오기 시작할테니 기대해도 좋다.

1.5 Definition

$S$를 어떤 집합이라고 하자. 어떤 order는 $S$에서 정의 되는 관계로, $<$ 기호로 표현되며 다음과 같은 두 가지 성질을 만족한다.

1. 만약 $x\in S$이고 $y\in S$라면 이 세 가지 문장중 딱 하나만 참이다.

   \[\begin{align*} x<y, \qquad x=y, \qquad y<x \end{align*}\]

2. 만약 $x,y,z\in S$이고, $x<y$ 이면서 $y<z$ 라면, $x<z$ 이다.

$x<y$ 대신 $y>x$라고 쓰기도 한다. $x\leq y$라고 쓰는 것은, $x<y$ 이거나 $x=y$임을 나타내며, 둘 중에 정확히 어떤 것이 참인지를 표현하지는 않는다. 달리 말하자면, $x\leq y$는 $x>y$의 부정문이다.

해설

이 내용은 아마 대부분의 사람에게 익숙한 내용일 것이다. 부등호와 등호는 초, 중학교 때 배우고 오는 개념이기 떄문이다. 지체하지 않고 바로 다음 정의로 넘어가도록 하겠다.

1.6 Definition

ordered set은 order가 정의된 집합이다.

해설

ordered set이라는 용어는 단어가 주는 느낌 그대로 order가 정의된 집합을 의미한다. 책에 나온 예시로 설명하면, 임의의 유리수 $r$과 $s$에 대하여 $s-r$이 양의 유리수를 의미하도록 $r<s$를 정의하면, 유리수 $\mathbb{Q}$는 ordered set이다.

1.7 Definition

$S$가 ordered set이고, $E\subset S$라고 하자. 어떤 $\beta\in S$가 존재하여 모든 $x\in E$에 대하여 $x\leq\beta$를 만족시키면, $E$가 bounded above라고 하며, $\beta$를 $E$의 upper bound라고 한다. lower bound는 위의 정의에서 $\leq$ 기호를 $\geq$ 기호로 바꾸면 정의된다.

해설

슬슬 낯선 단어가 나오기 시작한다. 우선 이 정의에서는 $E$의 upper bound와 lower bound가 무엇인지를 정의하는데, bound라는 단어는 경계라는 의미를 가지고 있으며, upper bound는 말 그대로 위에 있는 경계, lower bound는 아래에 있는 경계를 의미한다. $E$의 어떠한 원소도 upper bound보다 클 수 없으며, lower bound보다 작을 수 없다.

1.8 Definition

$S$가 어떤 ordered set이라고 하고, $E\subset S$이며, $E$가 bounded above되어 있다고 하자. 다음 성질들을 만족하는 $\alpha\in S$가 존재한다고 할 때,

1. $\alpha$는 $E$의 upper bound이다.
2. $\gamma < \alpha$인 경우 $\gamma$는 $E$의 upper bound가 아니다.

$\alpha$를 $E$의 least upper bound 또는 supremum 이라고 부르며, 다음과 같이 쓴다.
\[\alpha=\sup E\]

$E$의 greatest lower bound 또는 infimum 도 같은 방식으로 정의된다.
\[\alpha=\inf E\]

가 의미하는 바는 $\alpha$는 $E$의 lower bound이며, $\beta>\alpha$일 때 $\beta$가 $E$의 lower bound인 것은 없다는 것이다.

해설

드디어 점점 머리가 아픈 내용이 나오기 시작한다. 갑자기 알파, 베타, 감마 같은 그리스 문자들이 튀어나오고 어려운 영어 단어들이 우리에게 공포를 선사한다. 하지만 그 말을 천천히 뜯어 보면 그렇게까지 어려운 개념은 아니다.

least upper bound라는 용어를 뜯어보면, ‘가장 작은 위에 있는 경계’라는 말이된다. 이게 무슨 말이냐 하면, 위에 있는 경계는 경계인데, 그 경계 들중 가장 작은거라고 생각하면 된다. 이해를 돕기 위한 설명을 하자면, 위에서 아래로 뚜껑을 덮는 느낌을 상상하면 된다.

물이 가득 담긴 병을 상상해 보아라. 그 위에 뚜껑을 덮으려고 하는데, 뚜껑을 너무 아래로 내려버리면 물이 넘쳐버릴 것이다. 그래서 위에서 천천히 내려오는 방식으로 뚜껑을 덮는데, 공중에 있는 동안은 upper bound이되, least upper bound는 아니다. 뚜껑을 아직 더 내릴 수 있기 때문이다. 물 표면까지 내려와 딱 닿는 순간의 이미지를 least upper bound의 느낌으로 생각하면 된다. 여전히 뚜껑은 물 위에 있지만, 더 내려가는 순간 수면의 높이보다 뚜껑의 위치가 낮아져 물이 넘치는 것이다.

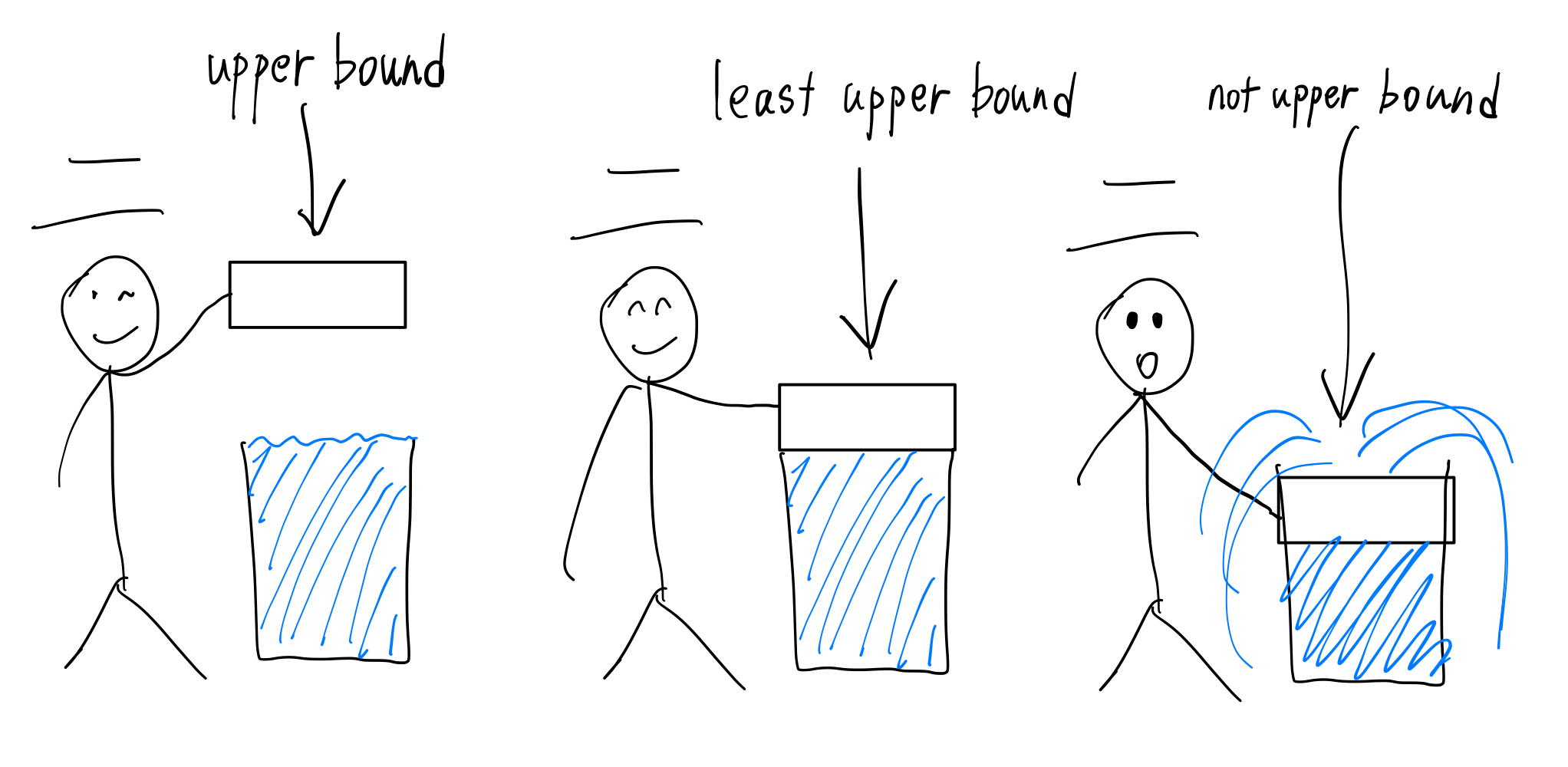
greatest lower bound도 비슷한 느낌으로 이해하면 될 것 같다. 그냥 아래에서 뚜껑을 덮는걸로만 바꾸면 얼추 비슷한 느낌인 것이다.

다음에 나오는 1.9 예시에서는 1.8에서의 정의를 활용하여 몇 가지 집합에서 이 개념들이 어떻게 적용되는지를 설명한다.

1.9 Examples

1. Example 1.1의 집합 $A$와 $B$를 ordered set인 집합 $\mathbb Q$의 부분집합이라고 가정하자. 집합 $A$는 bounded above 되어있다. 실제로, $A$의 upper bound 들은 정확히 $B$의 원소이다. $B$에는 가장 작은 원소가 없으므로, $A$는 $\mathbb Q$ 에서 least upper bound 를 가지지 않는다.

   비슷하게, $B$는 bounded below 되어있다. $B$ 의 모든 lower bound 의 집합은 $A$ 와 모든 $r \le 0$ 인 $r \in \mathbb Q$ 로 구성되어 있다. $A$ 에는 가장 큰 원소가 없으므로, $B$ 는 $\mathbb Q$ 에서 greatest lower bound 를 가지지 않는다.

2. 만약 $\alpha x = \sup E$ 가 존재한다면, $\alpha x$ 는 $E$ 의 원소일 수도 있고, 아닐 수도 있다. 예를 들어, $E_1$ 를 $r < 0$ 인 $r \in \mathbb Q$ 들을 모아놓은 집합이라고 하자. 그리고 $E_2$ 를 $r \le 0$ 인 $r \in \mathbb Q$ 들을 모아놓은 집합이라고 하자. 그러면 아래의 식이 성립한다.

   [ \sup E_1 = \sup E_2 = 0. ]

   그리고 우리는 $0 \notin E_1$ 이지만, $0 \in E_2$ 라는 사실을 확인할 수 있다.

3. $E$ 를 $n = 1, 2, 3, \cdots$ 에 대하여 $\frac{1}{n}$ 들을 모아놓은 집합이라고 하자. 그러면 $\sup E = 1$ 이고, 이는 $E$ 에 포함되어 있으며, $\inf E = 0$ 이고, 이는 $E$ 에 포함되어 있지 않다.

해설

1. (WIP)

2. (WIP)

3. (WIP)

1.10 Definition

어떤 ordered set $S$는 다음의 성질을 만족할 떄, least-upper-bound-property를 만족한다고 한다:

만약 $E\subset S$이고, $E$가 공집합이 아니며, $E$가 bounded above 되어있으면, $\sup E$는 $S$에 존재한다.

해설

이 부분의 정의가 무슨 말을 하는건지 조금 헷갈릴 수 있다. $S$가 least-upper-bound-property를 가지고 있다는 것은, $S$의 부분집합인 $E$가 특별한 성질을 가지게 된다는 것을 의미한다.

그 특별한 성질이 무엇인가 하면, $S$에서 가져온 부분집합 $E$가 운좋게도 공집합이 아니면서 bounded above 되어있다면, 그 부분집합 $E$의 least upper bound가 존재하고, 그것이 $S$에 포함된다는 것이다.

만약 기껏 $E$를 뽑긴헀는데, 공집합이거나 bounded above 되어있지 않다면, 이 정의에서는 딱히 할 수 있는 이야기는 없다. (이 정의에서가 아니여도 달리 할 수 있는 이야기가 뭐가 있을지는 나도 잘 모르겠다.)

여기서 한 가지 의문이 들게 된다. least-upper-bound-property라는게 있다면, greatest-lower-bound-property는 없는가? 그것에 대한 이야기가 다음에 오는 Theorem 1.10이다.

1.11 Theorem

$S$가 least-upper-bound-property를 지닌 ordered set이라고 가정하자. $B\subset S$이고, $B$가 공집합이 아니며, $B$가 bounded below 되어있다고 하자. $L$이 $B$의 lower bound들을 모두 모아놓은 집합이라고 하자. 그렇다면,
\[\alpha = \sup L\]

이 $S$에 존재하며, $\alpha = \inf B$이다. 달리 말하면, $\inf B$는 $S$에 존재한다.

해설

이 Theorem이 말하고자 하는 것은 least-upper-bound-property를 가진다는 것은, 동시에 greatest-lower-bound-property를 가진다는 것을 의미한다는 것이다. 그걸 동시에 가진다는게 말이나 되나 싶을 수 있지만, 놀랍게도 이게 된다. 아래는 그 증명이다.

증명

우선 $L$에 대하여 차근차근 뜯어보면서 이걸 증명해보자. 일단 $L$은 $B$의 lower bound들의 집합이라고 했는데, $E\subset S$이고, lower bound들은 정의 1.7에 따라서, 모두 $S$에 포함되어 있다. 또한, $B$가 bounded below 되어있다고 했으니, 하나라도 lower bound가 존재한다는 것을 의미하고, 그것은 $L$이 공집합이 아니라는 것을 말해준다. 또한 $B$에서 아무 원소 $b$를 잡고, $L$에서 아무 원소 $l$을 잡아도, lower bound의 정의에 의해서 항상 $b\geq l$ 이다. 이 말을 다시 살펴보면, $L$의 모든 원소 $l$은 어떤 $b\in B\subset S$ (따라서 $b\in S$)에 대하여 $l\leq b$ 이므로, $L$은 bounded above 되어 있다.

우리가 방금 얻어낸 중요한 정보는 총 3개이다.
1. $L\subset S$이다.
2. $L$은 empty set이 아니다.
3. $L$은 bounded above 되어있다.

어디서 많이 본 조건들이 아닌가? 그렇다. 정의 1.10에서 우리는 이 조건들은 본적이 있고, $S$는 least-upper-bound-property (지금부터는 LUBP로도 부르겠다.) 를 지닌 ordered set이므로, 정의에 따라 $sup L$은 $S$에 존재한다. 우리는 방금 $\alpha = \sup L \in S$임을 보인것이다!

이제 남은 과제는 $\alpha = \sup L = \inf B$ 임을 보이는 것이다. 그렇다면 이 Theorem을 증명하는데 성공하게 된다. 말로 풀어서 말하면, $L$의 supremum이 $B$의 infimum이라는 것을 증명하기만 하면 모두 끝난다는 것이다.

여기서 우리는 귀류법을 사용할 것이다. 우선, 결론을 부정하여 $\alpha = \sup L \neq \inf B$라고 해보자. 정의 1.8에 따라서, $\alpha$가 $B$의 lower bound가 아니 '거나' (OR), $\beta > \alpha$ 일 때 $\beta$가 $B$의 lower bound인게 있다는 의미이다.

우선 첫 번째 조건을 살펴보자. $\alpha$가 $B$의 lower bound가 아니라는 부분인데, 우리는 이 조건이 틀렸다는 것을 보여야 한다. $L$은 $B$의 모든 lower bound들을 모아둔 집합이기 때문에 $\alpha \in L$라는 것만 보일 수 있다면 이 조건은 쉽게 틀렸다는 것을 보일 수 있다. 그렇다면 어떻게 $\alpha \in L$임을 보일 수 있을까?

여기서 우리는 supremum의 정의를 한 번 더 살펴보도록 하겠다. 정의 1.8에 따라 $\gamma<\alpha$라면, $\gamma$는 $L$의 upper bound가 아니게 되고, 이는 $\gamma \notin B$임을 의미한다. 거꾸로 말하면, $\gamma \in B$ 라면 $\gamma$가 $L$의 upper bound이고, 이는 $\alpha \leq \gamma$임을 의미한다. 따라서, $\alpha$는 $B$의 lower bound이고, $\alpha\in L$이다. 이로써 우리는 첫 번째 조건이 거짓임을 보였다. 그러나 두 조건이 'or'로 연결되어 있기 때문에 우리는 두 번째 조건인 $\beta > \alpha$ 일 때 $\beta$가 $B$의 lower bound인게 있다는 조건이 거짓임을 한 번 더 보여야 한다. 여기서 귀류법을 한 번 더 사용하도록 하겠다. 그런 $\beta$가 존재한다고 가정하자. $\beta$는 $B$의 lower bound이기 때문에 $\beta \in L$ 이고, $\alpha = \sup L$이기 때문에, 정의에 따라 $\beta \leq \alpha$ 이다. 이는 우리가 처음에 가정했던 $\beta > \alpha$라는 것과 모순된다. 따라서 두 번째 조건도 거짓임을 밝혔다. 두 조건이 모두 거짓임으로, 다시 말해 $\alpha$가 $B$의 lower bound가 '아닌 것'도 아니고, $\beta > \alpha$ 일 때 $\beta$가 $B$의 lower bound 인게 없다. 이는 우리의 가정과 모순되므로, $\alpha = \sup L = \inf B$이다. $\alpha = \sup L \in S$ 이고, $\alpha = \sup L = \inf B$ 이므로, 당연히 $\inf B \in S$ 이다. $\blacksquare$

이걸로 Ordered Set 단원이 마무리 되었다. 이 단원에서는 order, ordered set, bounded above, bounded below, upper bound, lower bound, least upper bound (supremum), greatest lower bound (infimum), least-upper-bound-property가 무엇인지 정의하였고, least-upper-bound-property를 가진 ordered set은 greatest-lower-bound-property 또한 가짐을 증명하였다.

대체 이런 용어를 왜 정의하는가 이해가 잘 안될 수 있다. 이런 걸 정의한 이유는 쉽게 말하자면 다음 단원들에서 쓰기 때문이지만, 필자는 이렇게 생각한다. 기존에 사용하던 최대값과 최소값의 개념을 확장한 느낌으로, 최대값과 최솟값이 정의되지 않는 집합들에서도 어떤 ‘경계’를 정의할 수 있도록 새로운 개념을 만들고 특징을 확립한 것이다.

그렇게 생각하면 기존의 익숙한 개념을 좀 더 다양한 곳에서도 비슷하게 적용할 수 있게 하기 위해서 의미를 확장했을 뿐인 것이다. 그렇게 생각하면 마냥 낯설고 이상한 뻘짓은 아니라는 것을 알 수 있을 것이다. 이 소단원이 그러한 활동의 첫걸음인 것이다.

그러나 해석학의 진정한 묘미는 여기서 시작된다. 기존의 개념을 확장하여 다른 곳에서도 비슷하게 사용되도록 새롭게 개념을 정의하게 되면, 기존의 영역에서 당연이 통용되던 성질이, 사실은 당연하지 않다는 사실을 깨닫게 될 것이다. 또한, 해석학은 엄밀하고 튼튼한 논리를 기반으로 전개되기 때문에, 공부하는 과정은 어렵고 고통스러워도, 그 과정이 모두 끝나 어떤 내용을 이해하게 된다면 엄청난 지적 희열을 느낄 수 있을 것이다.

마무리

원래 오늘 계획은 1단원을 모두 마무리 하는 것이였다. 그러나 책의 텍스트 양도 많고, $\LaTeX$ 문법을 이용하여 타이핑을 하는 것은 고된 작업이라 그런지, 고작 2개의 소단원 밖에 다루지 못했다. 아쉽긴 하지만, 다른 소단원의 내용들은 내일 더 다루도록 하겠다.

마지막으로, 오늘 배운 내용들을 간단하게 요약해보겠다.

1. 유리수로는 못 나타내는 수가 많아서 실수가 필요하다.
2. 실수를 정의하기 위해서는 ordered set과 field의 개념이 필요하다.
3. ordered set을 정의하면서 기존의 최대값과 최솟값의 개념을 확장한 supermum과 infimum을 정의하였다.
4. 시간이 부족해서 field의 정의부터는 내일 이어서 하겠다.

오늘의 공부는 여기까지!

---

---