블로그에 관하여

수정사항

블로그에 이제 다양한 이미지를 넣기 시작하면서, 날짜별로 폴더를 만들게 되면 나중에 관리하기 너무 어려워지게 될 것이라고 생각했다. 그래서 연도별 폴더 내부에 월별 폴더들을 만들고 월별 폴더 내부에 각 날짜의 폴더를 만드는 구조로 변경했다. 특정 기간에 자주쓰이는 이미지들은 월별 폴더나 연도별 폴더에 별도의 하위 경로를 생성하지 않고 넣으면 일일히 날짜별 폴더에 사진을 붙여넣지 않아도 될 것이다.

덕분에 글에서 설정한 그림의 경로가 전부 바뀌어 이 글을 제외하고 4개의 글들의 경로를 수정해주었다. 그 과정에서 어제 올린 글의 사진이 지나치게 크게 나오는 것을 확인할 수 있었다. 그래서 HTML태그를 이용하여 사진을 넣었고, 그림이 적당한 크기로 나오게 설정할 수 있었다.

B-Tree 프로젝트

오늘은 B-Tree에서 키값을 삽입하는 Insert에 대해서 이야기 하도록 하겠다. 여느 때와 마찬가지로, Wikipedia¹를 기준으로 설명하겠다.

B-Tree의 Insert

B-Tree에서 삽입은 리프 노드에서 시작된다. 새로운 키값을 삽입하기 위해서는, 그 키값이 추가될 리프 노드를 찾는 것 부터 시작된다. 해당 노드에 값을 삽입하는 과정은 두 가지 경우 중 하나를 따른다.

만약 그 노드가 포함할 수 있는 최대의 요소 개수, 즉 그 B-Tree의 (order-1)보다 적은 개수의 요소를 포함하고 있다면, 해당 노드에 새로운 요소를 포함할 공간이 있음을 의미한다. 그러므로 노드 내부의 요소들이 정렬된 상태를 유지하게끔 해당 키값의 삽입을 진행한다.
만약 노드의 요소가 가득 찬 상태라면, 노드 분할이 발생한다. 노드 분할은 다음과 같은 순서를 따른다.
1. 해당 리프 노드의 요소들과 삽입하고자 하는 키값들 중 ‘중앙값’을 선택한다.
2. 해당 중앙값을 기준으로, 작은 값들은 왼쪽의 새로운 리프 노드에, 큰 값들은 오른쪽의 새로운 리프 노드에 둔다.
3. 그 중앙값은 기존의 리프 노드의 부모 노드에 삽입되고, 이 경우에도 ‘삽입’이 발생하기 때문에 추가적인 노드 분할이 발생할 수 있다. 만약 부모 노드가 존재하지 않는다면, 다시 말해 분할이 일어난 노드가 루트 노드라면, 새로운 노드를 생성하고 그 노드에 삽입을 진행하게 된다. 이 경우 트리의 높이가 증가하게 되며, 새롭게 생성된 노드가 루트 노드가 된다.

백문이 불여일견

늘 그래왔듯, 설명만 읽어봐서는 정확히 무슨 말인지 이해하기 어려울 것이다. 그래서 이번에도 직접 B-Tree에서 특정한 값을 삽입하는 예시를 통해 앞서 설명한 내용들을 다시 풀어서 설명할 것이다.

예시

아래 그림과 같은 B-Tree를 생각해보자. 25개의 원소를 가진 B Tree

이 B-Tree는 order가 $3$인 B-Tree이며, 총 25개의 키가 저장되어 있다. 이 B-Tree에 21, 14를 순서대로 삽입해보고, 그 과정을 따라가보겠다.

1. 21 삽입하기

이 B-Tree에 21을 삽입하기 위해선 21이 삽입될 리프 노드를 우선 탐색해야 한다. 어제 다루었던 B-Tree에서 Search를 수행하는 방식을 활용하여 리프 노드를 찾을 수 있다.

오른쪽 subtree의 왼쪽 subtree

그림에서 확인할 수 있는 것 처럼, $(20,-)$ 노드에 삽입을 진행할 수 있다. 현재 이 리프 노드에 포함된 요소의 개수는 1개로, 이 B-Tree는 order가 $3$이기 때문에, 최대 2개의 요소를 포함할 수 있다. 따라서, 21이 들어갈 공간이 확보되어 있는 상태이므로, 남은 공간에 21을 삽입한다.

21 삽입완료

이 B-Tree에 21이 성공적으로 삽입되었음을 확인할 수 있다.

2. 14 삽입하기

이 B-Tree에 14을 삽입하기 위해선 앞에서와 마찬가지로 14가 삽입될 리프 노드를 우선 탐색해야 한다. B-Tree에서 Search를 수행하는 방식을 활용하여 리프 노드를 찾을 수 있다.

가운데 subtree의 가운데 subtree

그림에서 확인할 수 있는 것 처럼, $(13,15)$ 노드에 삽입을 진행할 수 있다. 현재 이 리프 노드에 포함된 요소의 개수는 2개로, 이 B-Tree는 order가 $3$이기 때문에, 최대 2개의 요소를 포함할 수 있다. 따라서, 14이 들어갈 공간이 확보되어 있지 않기 때문에, 노드 분할을 진행한다.

리프 노드의 중앙값은 14

우선 리프 노드의 요소들과 삽입하고자 하는 키값의 중앙값은 14이다. 기존의 리프 노드를 분할하여 새로운 리프 노드 2개를 만들고 중앙값보다 작은 13은 왼쪽의 리프 노드에, 15는 오른쪽의 리프 노드에 둔다. 그리고, 부모 노드인 $(12, 16)$에 14를 삽입한다.

첫 번째 분할

이 때, 기존의 $(12, 16)$ 노드는 이미 요소가 가득 찬 상태이므로, 14를 수용할 공간이 없다. 따라서, 다시 한번 분할이 발생해야 한다. 중앙값으로 14를 선택하고, 기존의 리프 노드를 분할하여 새로운 리프 노드 2개를 만든다. 중앙값보다 작은 12는 왼쪽의 리프 노드에, 16은 오른쪽의 리프 노드에 둔다. 그리고, 부모 노드인 $(9, 19)$에 14를 삽입한다.

두 번째 분할

이 때, 기존의 $(9, 19)$ 노드는 이미 요소가 가득 찬 상태이므로, 14를 수용할 공간이 없다. 따라서, 또 다시 한번 분할이 발생해야 한다. 중앙값으로 14를 선택하고, 기존의 리프 노드를 분할하여 새로운 리프 노드 2개를 만든다. 중앙값보다 작은 9는 왼쪽의 리프 노드에, 19는 오른쪽의 리프 노드에 둔다. 이 때, 이 노드는 루트 노드로, 부모 노드가 없다. 따라서, 새로운 빈 노드를 만들고, 14를 삽입한다.

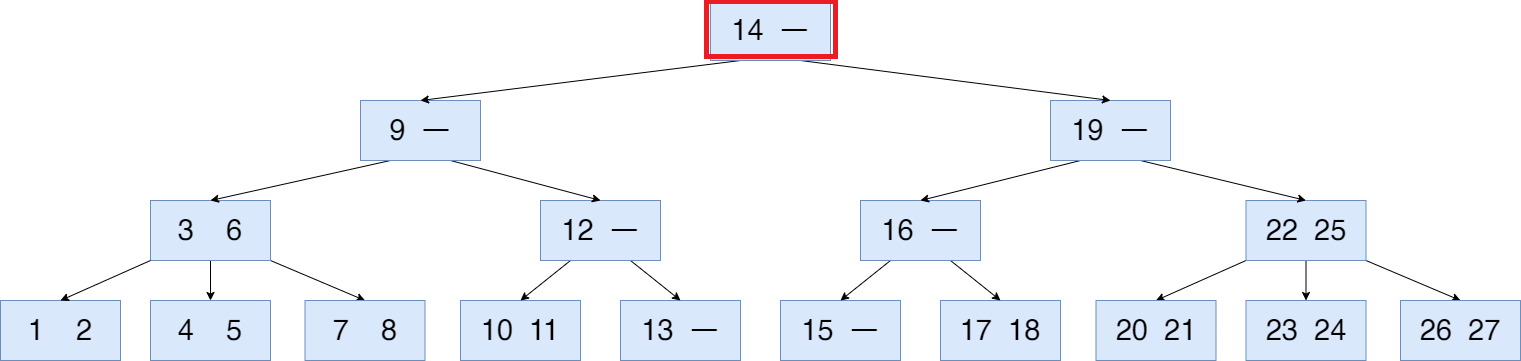
세 번째 분할

이 때 새롭게 만들어진 노드가 기존의 루트 노드의 부모 노드가 되며, 이제 이 B-Tree의 루트 노드는 이 노드가 된다.

오늘은 여기까지

오늘은 B-Tree에서 Insert가 무엇인지, 어떻게 작동하는지 알아보았다. 내일은 B-Tree에서 어떤 키값을 Delete하는 방법에 대해서 알아보도록 하겠다. 또한, 새로운 키값을 Delete하는 과정에서 발생하는 여러 가지 상황에 대해서도 알아볼 것이다.

마무리

오늘은 여기서 글을 마무리 하겠다. 잡담 쓸만한게 오늘도 딱히 떠오르지 않고 ‘오늘’도 별로 안남았다.

오늘의 개발은 여기까지!

1: https://en.wikipedia.org/wiki/B-tree

← Previous Post Next Post →

B-Tree에 대하여 - 3

B-Tree에서 키를 넣는 법